Astrophysics Part V: The End of the Universe

Andromeda Galaxy

So we have considered the evolution of stars, and evidence supporting the big bang, however, we have not yet covered the end of our universe.  This topic has, like many  phenomena of astrophysics been debated over for many years.  There are multiple theories, but all of them depend on the mass of the universe.  The universe could be either

• Closed
• Open
• Flat

Possible Fates of the Universe

A closed universe means that gravity will stop the universe from expanding, causing it to contract, this would result in a massive contraction of the universe in a big crunch, from which the universe could begin again.  The density of the universe would have to exceed the critical density, ρ > ρ_c.

An open universe means that gravity would be too weak to stop the expansion.  The universe would expand forever, the density of the universe would be less than the critical density thus ρ < ρ_c.  The universe will end in either a big rip or big freeze.  In the big rip, acceleration of the expansion of the universe caused by the presence of dark energy would become too large, and would supersede the strong nuclear force, the electromagnetic and gravitational forces, resulting in the reduction of all matter to elementary particles.  However, the possibility of a big freeze is also possible.  As the universe expands, the concentration of dust and gas clouds would decrease, and the fuel needed for star growth would decrease as well.  This would result in less stars from forming.  Furthermore, the extreme redshift of electromagnetic waves, would leave the waves with little energy.  Meanwhile, the distance between galaxies would be rapidly increasing.  The universe would be unable to sustain life, as Earth would become too cold.

Lastly, the universe may be flat.  The density is equal to the critical value, consequently the universe will only begin to contract after an infinite amount of time. This means that the universe’s density must equal critical density, ρ = ρ_c.  The fates of the universe would be the same as an open universe.

Astrophysics Part IV: Redshift and the Expanding Universe

Nowadays the universe is believed to have began with the big bang. The universe began from a singularity, a spot of infinite density where the four fundamental forces, gravity, the strong and weak nuclear forces, and the electromagnetic force were united. Before this explosion, time and space did not exist.

However, for many years, it was thought that the universe was static, stationary and infinite.  In fact the great physicist and mathematician, Isaac Newton believed this as well, arguing that unless this was correct, the universe would become a spherical mass, as all the stars would have been attracted together, by gravitation.  But it was a German amateur astronomer, Henrich Olber, who disproved Newton’s theory.  The famous Olber’s paradox states that if the universe was infinite and stationary, then the whole sky would be bright.  If one was to look at any direction the night sky would be bright because, there would be an infinite number of stars in any given direction. This can be mathematically shown by a simple proof.

Imagine the stars are distributed in a layer with a density of ρ, thus the number of a stars would seem to be the density, ρ, multiplied by the thickness of the layer, d, multiplied by the surface area of the layer, which is that of a sphere, 4πR². Thus the number of stars that would be visible would be 4πR²ρd.  The volume of visible stars would increase by R², however, luminosity would decrease by 1/R².  Thus luminosity would be equal anywhere. The distance of R² would cancel out, leaving the luminosity to be 4πρd, which would only depend on the thickness d, and the density ρ, not on the location of the observer.

The night sky however, is dark and thus we can conclude that the universe is not infinite or static, but changes with time. The big bang model states that the universe is constantly expanding, and that the distribution of stars is not uniform, resolving Olber’s paradox. However there are many other factors which support the big bang. The first is redshift. This is a phenomena which occurs with radiation emitted from stars that are moving away from us. This is similar to the Doppler Effect.

The Doppler Effect: The changing of frequency which arises from the relative motion between a source and observer

However, the rarefaction or stretching of light waves is actually not due to the Doppler Effect, instead it is due to the fabric of spacetime itself increasing.  Since the big bang, the universe has been increasing in size.  If a photon leaves a nearby galaxy, it spends a considerable time in space. But the space where it is moving is actually being increased in size, thus the longer a particle spends travelling in space, the more the light is rarefacted. As electromagnetic radiation travels at a constant speed, the amount of redshift can be use to determine how far away an object is, and also suggests to us that the universe is expanding. When the particle reaches us, it will have been redshifted, showing us how the universe is expanding, from a central point, suggesting the big bang model is correct.

This relationship can be expressed mathematically by the formula,

Δλ/λ=v/c

Where Δλ = λ’- λ, where λ is the wavelength from a stationary source, and λ’ is the wavelength measured from the source that is moving at speed v , and c is the speed of light

The third factor which supports the big bang is to do with the amount of helium in the universe. In fact 24% of the universe is helium, but the percentage is too high to be solely produced by fusion in stars, suggesting that the helium was made elsewhere. Two physicists, Dicke and Peebles, suggested that this helium was formed in the early universe, when temperatures were large enough to allow hydrogen fusion. In these reactions, high energy photons would have also been produced.  But when later, two physicists Penzias and Wilson positioned an aerial facing space, they encountered constant cosmic background radiation that seemed to have been emitted from a black body of only 2.726K.  (Click this link for information about Wien’s Law) However, the temperatures for hydrogen fusion would have been much larger than this.  The wavelength of this radiation must have increased, supporting the idea of an expanding universe once more, and the big bang.

There are numerous other factors which support the big bang, such as the existence of quasars, and large gas clouds. To summarise we will list the three factors which support the big bang model, which you may have to list in an exam paper.

The three factors which support the Big Bang model

• Olber’s Paradox
• Redshift / The Expanding Universe
• Amount of Helium / Cosmic Background Radiation

Astrophysics Part III: Stellar Evolution and the Different Types of Stars

In our previous two articles we have covered basic topics of astrophysics such as stellar clusters and apparent brightness. In this article we will exploring the more complicated, the evolution of a star, and exploring the different possible paths a star’s evolution can take. The sun is the nearest star to Earth, and without it, life would not be able to exist.  Our planet is held in orbit by this star, however, eventually the sun will expand and engulf our planet.  This article will look at the evolution of stars and the different names for different stages of a star’s life.

A Planetary Nebula

Stars, surprisingly, begin as nebulas, clouds of dust and gas in space.  Gravitation brings the particles together, which increases the temperature of the particles and also ionises them, and they produce light.  At this point it becomes a protostar, which is very large and can have a surface temperature of 3000K.  However, at this point it is much larger than a star with similar mass, and the gravitation continues, decreasing the volume of the star.  The contraction continues until the core has become completely ionised plasma. Nuclear fusion begins converting the hydrogen in the core to helium, the protostar is now a star, which can be found on the Hertzsprung-Russel diagram. As described in our earlier post, the Introduction to Astrophysics, the gravitational pressure and radiation pressure are equal.

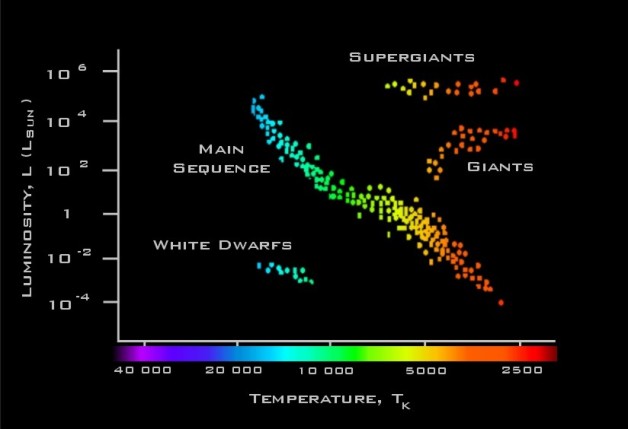
A Hertzsprung-Russel Diagram

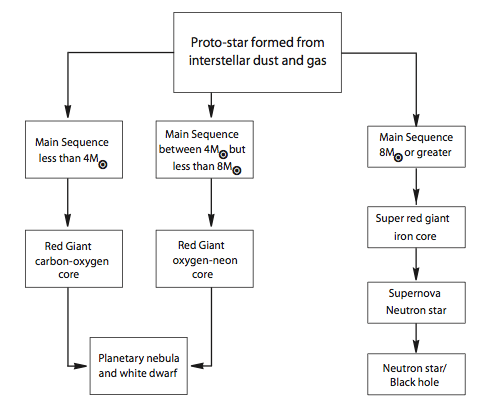
The larger the mass of the star the greater its luminosity and temperature, stars can be found in the main sequence. The size of the original mass of the star determines how long its time on the main sequence is.  Our sun, is actually a relatively small star, and will burn for approximately 10¹⁰ years, however, a star with a mass of 25 times our sun’s will have burn its hydrogen core for only 10⁶ years. After this is complete, the star leaves the main sequence, becoming a red giant. The fusion in the core has stopped and now with no opposing forces the gravitational contraction increases the temperature of the core, and the outer layers of the star. As the outer layers increase in temperature, the star expands, the luminosity increases, but surface temperature decreases.  Helium is created from the fusion of hydrogen, and this causes to core to further contract, until the temperature becomes so high that helium becomes to fuse, to produce Oxygen-16 and Carbon-12.  The process is repeated. Surprisingly, as the core decreases, the size of the star increases.

Once the fusion of helium in the core is complete, the core contracts again increasing the temperature of the outer layers, allowing helium fusion.  This is the second red giant phase,  and when the sun goes through this phase, it will likely engulf Earth. During this phase however, the outer layers of the star are expelled, exposing its hot core.  The 100000K core ionises the outer layers, causing them to emit visible radiation.  This stage is called a planetary nebula.  However, if the mass of the star is between 4-8 solar masses, it is possible to produce heavier elements through fusion, namely neon, sodium, oxygen and magnesium. The lack of fusion causes the core to cool, and the sun becomes a white dwarf cooling down and out of sight.

This however, can only occur if the mass of the core is less than 1.44 solar masses.  At 1.44 solar masses, the gravitational contraction force is at equilibrium with electron degeneracy. This is the force of electrons repelling each other, when they are tightly packed together.  it exists because of the Pauli exclusion principle, which states that no two electrons can be in the same state. But if the core of the star is greater than 1.44 solar masses, the gravitational contraction force is greater than the electron degeneracy pressure, and the star becomes either a black hole or a neutron star. This is called the Chandrashekar limit. Whether it becomes a black hole, or stays a neutron star, will be discussed later in this article.

However if the mass of the star is above 8 solar masses, the process of fusion continues, once helium has been fused, carbon is created. Once all the carbon in the core is fused, the temperature rises to 10⁹ K, here neon is fused.  After this, the process repeats and oxygen is fused, producing silicon. Finally the temperature is large enough for the fusing of silicon, which produces iron, the most stable of all elements.  This is called a super red giant.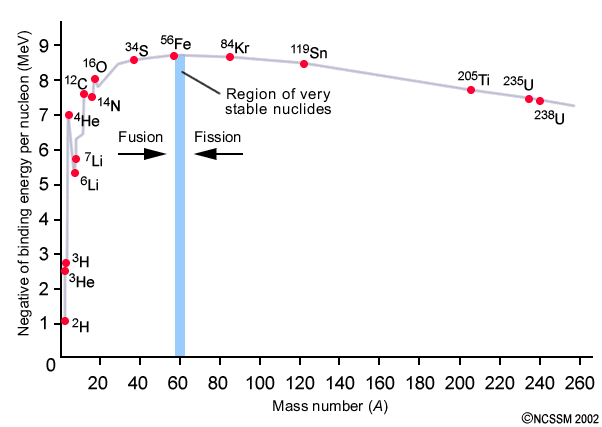 

Once the whole core is iron, it contracts rapidly, reaching a temperature of 6 x 10⁹ K.  High energy gamma photons, collide with the iron nuclei, breaking them into alpha particles.  Then the negative electrons and positive protons combine, producing neutrons and large quantities of neutrinos.  These carry energy away from the star, causing it to contract once more.  However, this rapid contraction creates produce a wave of pressure that moves outwards away from the centre of the star.  At the same time, because the core is contracting, matter is falling into the centre of the star, however, this is repelled by the outwards pressure wave. The wave accelerates, but soon reaches the speed of sound, becoming a colossal shock wave that rips the outer layers of the star apart.  This exposes the hot inner cores, and large amounts of radiation enter space.  The process is called a supernova.  Through this process 96% of the star’s mass is lost, and the material flung out into space forms nebulae, where new protostars can be created.

However, the stellar evolution is not yet finished. The remnant from the supernova has formed into neutrons, and these combine to form an extremely dense star called a neutron star.  The collapse is prevented by neutron degeneracy pressure.  If the mass is greater than between 2-3 solar masses however, a black hole is formed.  The figure is not precise, as the equations regarding extremely dense matter are not yet known. This marks the enter of the stellar evolution as we know it.

A neutron star is an extremely dense star, equal to the density of the whole human population packed into the size of a sugar cube. Neutron stars are typically small, and thus to conserve angular momentum must rotate.  This pheneomena is known as a pulsar. The rotating magnetic field of the pulsar produces radio waves, which are detectable from Earth. In fact, it was through these that pulsars were detected originally.

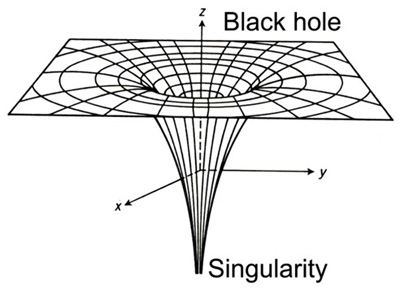
Now we will briefly look at black holes.  The earth has a gravitational constant of 9.81ms^-2, we can temporarily leave the surface if we jump, but gravity brings us back down.  However, if an object was so dense that this acceleration equalled to the speed of light, then nothing would be able to leave the surface of the Earth, not even light.  This is what we find in a black hole, and that is the reason why they are black, because nothing can escape then.  To picture this we must consider the fabric of space time. Large masses bend spacetime, however, if an object is so large, then space time will be bend around completely, preventing the escape of anything.  Even more interesting is the theory of General Relativity, which describes how in a gravitational field, time will slow down.  At points where the escape velocity equals to the speed of light, time ceases.  This is known as the event horizon.  Furthermore, when the entire mass of the star contracts into the event horizon, the density will be infinite. This is known as the singularity, where density is infinite.  A black hole consists of both a singularity and an event horizon.

The detection of black holes however, is difficult, as the phenomena does not emit radiation, and thus we cannot see them.  We have to look at the nearby stars, that may be having matter pulled off their surface, and radiation emitted by these types of processes.  Physicists believe their may be a black hole in the centre of our galaxy.

Arguments for Trade Protection

Trade protection occurs when a country’s government intervenes in international trade, imposing trade restrictions to prevent the free flow of imports into the country and protect the domestic economy from foreign competition

There are 4 main types of protectionist methods:

1. tariffs
2. quotas
3. production subsidies
4. administrative barriers

Although their methods vary, they all share the same effect of decreasing the number of imports, and increasing the quantity of goods and services domestically produced. However, one must consider the arguments for and against trade protection, to evaluate whether these measures can really be justified.  To start, we will look at the arguments for trade protection.

Infant industry argument

An infant industry is a new domestic industry that has only just established itself, not having the time to grow larger, and achieve economies of scale. Thus, the firms will have relatively low efficiencies, and be unable to compete with ‘efficient’ foreign firms. Without any type of production, the new infant industries would probably shut down, unable to compete and grow amongst much more efficient firms.  Arguably, trade protection should be utilised until the firm is large enough to achieve economies of scale. After first being introduced as an argument in 1791, the argument is primarily used now by developing countries trying to expand production. Economists consider this theory to be one of the strongest justifications for trade protection, possibly because it obeys the theory of comparative advantage,

The theory of comparative advantage states that along as opportunity costs in two (or more) countries differ, it is possible for all countries to gain from specialization and trade according to their comparative advantage; this results in an improvement in the global allocation of resources, resulting in greater global output and consumption.

The country in question may have a comparative advantage compared to another country, but first must receive protection. This can only be justified if the production is limited to a temporary period.  As soon as the infant industry can compete, the protection should be eliminated. However, this theory can also be misused and wrongly implemented.  Governments can misjudge different firms; wrongly deciding which firms could become low-cost producers. This also presents the opportunity for corruption and possible favouritism from governments.  Furthermore, once a firm is protected, it may not see the need to become efficient, forever existing as an ‘infant industry’. Similarly, a firm could protect an ‘infant industry’ long after it has achieved economies of scale.  The infant industry argument here has been purely reduced to a subsidy.

Strategic trade policy

This is similar to the infant industry argument, but the firms protected are slightly different.  High-technology firms are protected, as their presence is deemed important to the future growth of an economy.  There growth is assisted until they are large enough to compete for themselves.  This argument also applies to more developed countries, who may also aspire to increase their high technology industries. Here though the trade protection is not only limited to the traditional methods, but can also take the form of various supply-side policies, such as lower taxes, low-interest loans, and even government financing of research and developing.  However, along with the infant industry argument, there are also difficulties about who to protect, and also selecting appropriate protectionist measures.  Also, if many firms use this kind of protection at the same time, the idea of comparative advantage is made redundant. The protection could also last much longer than necessary, the government, continuing their protection for too long.

National Security

Some industries, such as aircraft, weaponry, chemical substances  and ores and minerals are believed to be beneficial for national defence, and thus are deemed necessary for protection, in the event of an attack.  In war, a country may have to rely on its own industries for defence, and thus industries which benefit national security should be protected.  Furthermore, in this sector, specialisation is discouraged.  For example, if a volatile or dangerous country specialises in weaponry, or a country is relied upon for aircraft, but then ends ties with other countries, the situation could be become dangerous. However, of course this theory for trade protection is subjective to each country.  Governments will differ in what they deem to be important to national security, however countries could also use this argument a façade, purely to subsidise products and employ trade protection.  For example, the United States protects goods such as candles, gloves and umbrellas, all in the name of national defence.

Health, safety and environmental standards

Countries have health, safety and environmental standards, that imported goods and services must meet before they can enter a country. Although each country can set its own standards, sometimes these standards can be used as a type of ‘hidden protection’, to keep some goods out, so they cannot compete with locally-produced goods.

Efforts of a developing country to diversify

Countries may employ trade protection on certain goods in order to diversify

Diversification: Generally refers to change involving greater variety, and is used to refer to increasing the variety of goods and services produced and/or exported by a country; it is the opposite of specialization.

In the past, the world has seen developing countries specialise in particular products, for example, Cuba in sugar and Ecuador in bananas. However, although this can yield both high quality and quantity of a good, arguments exist in favour of diversification. Listed below are some of the arguments for diversification.

• These goods which we have seen developing countries specialize in are generally primary sector goods.  However, as countries grow, manufacturing and services become progressively more important.  In developing countries, this is made possible by diversifying its range of goods and services into other sectors.

• Another reason for diversifying into manufacturing industry is that each step in production adds value to the good.  For example, in the extraction of metal ores, we see processes such as refining add value to the good, if developing countries not only manufacture but also extract, they can sell their products for higher prices and receive more revenue, resulting in economic growth.

• Primary goods also have much higher price volatilities than manufactured goods, and services, due the low price elasticities of demand and supply of such goods.  This can result in fluctuating wages for farmers, due to the low price stability of such goods. This is another factor supporting the diversification of goods.

Astrophysics Part II: Stars as Black Bodies and Wien’s Law

In the earlier post, I described the solar system, and introduced concepts such as luminosity and brightness. These two qualities, denoted as L and b, are also used in other equations, which describe the characteristics of stars. But first the concept of black body radiators must be introduced.

A black body is a hypothetical object which absorbs all incident electromagnetic radiation

The emission spectra of black bodies are related to the temperature of the body. As the temperature of the body is increased:

• the intensity of each wavelength increases
• the total energy emitted is higher
• the increase in intensity of shorter wavelengths is greater than the increase in intensity of longer wavelengths

A black body is hypothetically black at room temperature, however, at higher temperatures, the object would begin to emit thermal radiation and glow. Mathematically, this can be expressed as:

E∝T⁴

This equation shows the proportionality and is referred to as Stefan’s Law. A commonly referred to example of a black body is that of a box which has had its insides painted completely black. The box is completely sealed, but for a small hole made in one of the sides. When placed in a bright room, light would be able to enter the box. However when inside, the black walls would absorb the majority of the light when the light ray bounced off the walls. Only a small portion of the light would be reflected each instance, so there would only be a small chance of any of the light ever being reflected back out of the small hole. A diagram aids the explanation:

When written completely, the equation is:

L=4πR²σT⁴

Here, R refers to the radius of the concerned star, sigma σ refers to the Stefan-Boltzmann constant, which has the value 5.67×10^-8 W m^-2 K^-4. The units cancel when multiplied together, so the luminosity has the units of watts, denoted as W. Using the equation, we can determine the luminosity of a star.

Again using the concept of a black body, another equation called ‘Wien’s law‘ shows a relationship between the wavelength which is emitted with maximum intensity from the star, and the temperature of the star. This equation is used for all black bodies, and as stars are considered to be black bodies, the Wien’s Displacement Law can be used for stars as well.

Here, the intensity peaks when the wavelength denoted by the symbol lambda is at just over 2μm. This value of wavelength is used as the λ_max. Whenever we see such a graph, by observing the wavelength with peak intensity, this value is the λ_max. The relationship between λ_max and temperature T is inversely proportional.

T∝k/λ_max

here ‘k’ refers to a constant.

The actual value of this constant is 2.9×10^-3 m K, thus the equation can be written as an expression of T in terms of λ_max. The value for λ_max must be expressed in m. 

Using this equation, by observing a star’s spectrum, the temperature of it can be predicted.

Introduction to Astrophysics

This blog post seeks to explore the basics of the Astrophysics option for HL Physics.

Galaxies are vast collections of stars. The solar system is a name for the collection of eight planets which orbit our sun, excluding Pluto, which has has its star status removed. Some of these planets have moons, satellites which orbit the planet. For Earth, the only moon is The Moon. But for other planets, specifically the gas giants, Saturn, Jupiter, Uranus and Neptune they may have many moons, for example, Saturn has 18 moons and Jupiter has 16. Of all the planets, Jupiter has the greatest equatorial diameter, at 143000km, and the largest mass – 19000 × 10²³ kg.

A stellar cluster differs from a constellation.

A stellar cluster is a group of stars held together by the forces of gravitational attraction, whereas a constellation is a collection of stars that form a recognizable group from earth, that may not actually be close together in the sky.

An example of a constellation is the ‘big dipper’, and I have included a photo of this below.

As the distances involved in this topic are great, a measure of distance called the light year is used.

The light year is the distance light travels in a year, a distance of 9.46 × 10¹⁵m.

The main source of energy in stars is nuclear fusion. Inside the star, hydrogen is converted in helium, with high temperatures of 10⁷K and high pressure present. The atoms must overcome coulomb repulsion in order to get close enough to fuse. This may occur from the repulsion between the like negative charged electrons in the electron rings.

Stars keep their shape as there is a balance of radiation pressure and gravitational pressure. As the star is massive, the centre acts to attract the contents of the star inwards. However, this is balanced by the radiation pressure, which is an outward pushing force, acting from inside the star. Radiation pressure results from the continuos fusion reactions which take place. An image showing this is included below.

Now some important equations describing the characteristics of stars can be considered. Stars have nuclear reactions which produce energy. Stars can be classified by the amount of energy they produce per unit time.

The luminosity of a star is defined as the total energy emitted by the star per unit time, and is denoted as L. It has the unit of Watts (W).

The sun has a luminosity of 3.90 × 10²⁶ W.

The luminosity of a star can be used to calculate the apparent brightness, a measure of the power which takes distance from the star into account. As the distance between the star and the Earth increases, the intensity of the power received falls. Apparent brightness is a measure of the energy received per unit time per unit area at the surface of Earth, and is given by the equation:

The luminosity of a star is spread over the total surface area of a sphere of radius ‘d’. This is explained in the image below:

As the distance from the source of light increases, the power of A is spread over a larger and larger area. As the distance increases by a factor of 2, the brightness decreases by a factor of 4. When the distance is increased by a factor of 3, the brightness decreases by a factor of 9. This shows the inverse square law.  The apparent brightness can be measured using a device called a bolometer. If the distance d can be measured, then the luminosity L of the star can be determined.

Simple Harmonic Motion: Part One

In the IB physics syllabus, one of the more difficult topics is wave phenomena, in particular the concept of simple harmonic motion. Let us begin by reminding ourselves of the definition.

Simple Harmonic Motion is defined as periodic motion that takes place when the acceleration of an object is proportional to its displacement from its equilibrium position and is always directed toward its equilibrium position.

(Click the picture to see simple harmonic motion occurring)

The two conditions of SHM:

1. The acceleration is directed in the opposite direction to displacement, or towards the equilibrium position.
2. The size of the acceleration is proportional to the displacement from the equilibrium position.

Firstly, we know that the motion is repeated, from the word periodic. Furthermore,  as the object gets further away from the equilibrium position, the acceleration increases, and it always directs itself to the central equilibrium position.   Acceleration is in the opposite direction from the displacement from the equilibrium position. Considering a pendulum example, when the bob is left of the equilibrium position, the acceleration is directed right, in this sense it is a negative relationship.

In a pendulum, simple harmonic motion is exhibited.  Of course, we are ignoring the air resistance that dampens the motion. (Damping will be discussed at length in a later article).  As the bob of the pendulum moves in the path of an arc,  reaching its maximum positions, the accelerating force acting on it is greatest, and the velocity is zero, and as it passes through the mean position, the midpoint between the two extreme positions, the accelerating force acting on it is zero, but velocity is maximized. Here it is in equilibrium.

Terms used in simple harmonic motion

Now we must introduce some mathematics into the concept. But first we must consider the symbols that show certain quantities in simple harmonic motion:

Displacement: x_, which is a measure of the displacement of an object from its equilibrium position at any particular instant during an oscillation.
Amplitude: x₀, is a measure of the maximum displacement of an object from its equilibrium position during an oscillation
Period: T, is a measure of the time taken for the system to complete one oscillation.
Frequency: f, is a measure of the number of complete oscillations that a system makes in one second
Angular frequency: ω, is a measure of the rate that a simple harmonic motion oscillation covers 2π or 360°.  However, in SHM, we typically use radians as a measure of angles, so 2π is preferred.

Equations used in simple harmonic motion

The first equation we will be looking at is the relationship between the time period of one oscillation and the frequency of the oscillations of a system displaying simple harmonic motion:

or  

This shows that the frequency and the time period of an oscillation are in fact inversely proportional.

This brings us on to our second equation:

  or  

Here we have introduced the symbol, ω, which is a measure of the rotational speed of a system.  By substituting the first equation, which links frequency with time period we can form a new equation.

  or  

The next equation that shall be discussed is that which links acceleration of a simple harmonic oscillator to its displacement, this is the defining equation of SHM:

As previously described the acceleration is in the opposite direction from displacement, and thus there is a negative sign. When relative to the equilibrium position, the displacement is above or leftward, the acceleration would be directed below or rightwards. Furthermore, the angular frequency of the system is purely a constant of the simple harmonic oscillator, and thus we see that acceleration is dependent on the displacement.

Another equation concerning the acceleration is about the restoring force, which causes the acceleration into the equilibrium position.  This is given by the equation:

Once again, it is negative as if acceleration is in the opposite direction from displacement, the force must also be, as we can see this from the equation:

which shows that for a given mass, force is proportional to acceleration. Linking back to the previous equation, k is a constant to be found, but only in SHM systems that involve a spring, is k the spring constant.

This concludes the first article on simple harmonic motion.  The next article will delve more into the mathematics behind this phenomenon, and will also include graphs of displacement, velocity and acceleration of the oscillating object.

Demerit Goods

A demerit good is a good that is overprovided by the market and is deemed to be harmful for society.

These goods or services are considered to be harmful because they have great negative consumption externalities meaning that the consumption of these goods results in spillover effects on a third party and no compensation is paid.

An externality occurs when the actions of consumers or producers give rise to positive or negative side-effects on third parties, and these effects are not paid for or compensated for.

In a demerit good, the benefit to the personal consumer is greater than the benefit received by society, or MPB > MSB. This is a negative externality of consumption. The market is producing at Q_m, but from society’s point of view Q_opt is the preferable level of production. At Q_m, MSB≠MSC, this shows there is market failure, as allocative efficiency has not been achieved.

When allocative efficiency is achieved, the quantity of goods produced and consumed at Q_m, the market equilibrium quantity is not equal to  Q_opt, the quantity deemed most socially desirable. When allocative efficiency is achieved, resources are allocated so well, that if anyone was made better off another party would have to be made worse off.

In the diagram above, the pink triangle has been calculated as the welfare loss, and has been calculated by comparing community surplus at both Q_m and Q_opt and then subtracting the size of the externality up to the quantity of production Q_m. The use of community surplus as a measure of welfare will be discussed in future posts.

A good example of a demerit good is smoking, because the benefit gained by the  consumer is high, but the adverse effects on third parties are great. The externality includes passive smoking and the long term effects which may result from passive smoking, such as development of cancers. Obviously it is difficult to quantify the size of the externality, because when assessing the negative impact, there are elements such as pain or irritation which are difficult to assign a monetary value to.

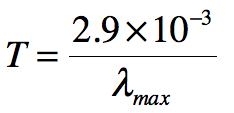
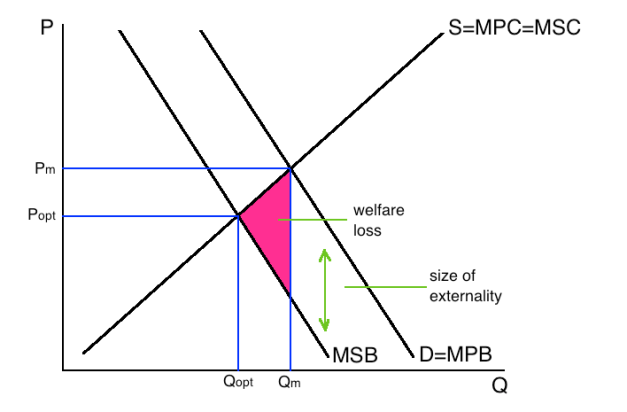
After government intervention, in this case negative advertising, a decrease in demand occurs and demand shifts left from D to D₁, meaning that the externality has decreased in size. Continuing the smoking example, on most cigarette packets the government enforces mandatory  negative advertising, such as pictures of cancers. After the decrease in demand, D₁ intersects S at a lower quantity, so Q₁ is now closer to Q_opt, meaning that the quantity supplied is now more favourable from society’s point of view. Thus the pink externality has decreased in size, meaning that society is less worse off.

An example of negative advertising, on an Australian cigarette packet.

Hello world!

Welcome to WordPress.com! This is your very first post. Click the Edit link to modify or delete it, or start a new post. If you like, use this post to tell readers why you started this blog and what you plan to do with it.

Happy blogging!